

Informática. Exame de Prácticas.
Setembro, 2006
Nome:
A derivada f'(x) dunha función real f (x) de variábel real no intervalo [a, b] defínese como:
Asemade, a integral definida de f (x) no citado intervalo se pode calcular, usando a regra dos trapecios, usando a expresión:
Onde n é o número de puntos da partición do intervalo [a, b]. A derivada f'(x) pódese aproximar numéricamente no intervalo [a, b] usando a expresión:
Onde h é o paso (con valor
h 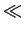 b - a). Pola outra banda, a integral definida
b - a). Pola outra banda, a integral definida
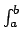 f (x)dx pódese aproximar mediante a expresión:
f (x)dx pódese aproximar mediante a expresión:
Onde n debe ter un valor elevado que simule que
n 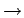
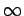 .
.
Debes escribir un programa en Fortran conteña o seguinte:
- (4 PUNTOS) Un un subprograma derivada(...) (debes decidi-lo tipo de subprograma), que reciba como argumentos dous valores reais a, b (extremos do intervalo no cal se calcula a derivada). A saída do subprograma deben ser tres vectores: un vector cos valores de x no intervalo [a, b] (
x = a, a + h, a + 2h, a + 3h,..., b), outro cos valores da función:
f (x) = 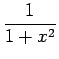
|
(5) |
nos valores de x e outro vector cos valores da súa derivada f'(x), aproximada usando a expresión 3.
- (3 PUNTOS) Outro subprograma integral_definida(...) (debes decidi-lo tipo de subprograma), que reciba como argumentos dous valores reais a, b (extremos do intervalo de integración). A saída do subprograma debe se-la integral definida da expresión 5 en [a, b], aproximada usando a expresión 4.
- (3 PUNTOS) Un programa principal que chame aos dous subprogramas anteriores, pasándolles como argumentos os extremos do intervalo [- 10, 10], para que calculen respectivamente a derivada e integral definida nese intervalo. Debes escribir tamén un subprograma chamado almacena(...) (debes decidi-los seus argumentos e tipo de subprograma), para que almacene os valores de x, f (x) e f'(x) no intervalo
x
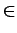 [- 10, 10] no arquivo datos.dat. Ao final do arquivo, este subprograma debe escribir o valor da integral
[- 10, 10] no arquivo datos.dat. Ao final do arquivo, este subprograma debe escribir o valor da integral
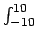 f (x)dx.
f (x)dx.



© 2006, Dr. Manuel Fernández Delgado, Universidade de Santiago de Compostela, Departamento de Electrónica e Computación
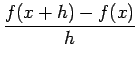 x
x 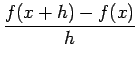 x
x 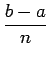
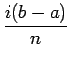
![]() b - a). Pola outra banda, a integral definida
b - a). Pola outra banda, a integral definida
![]() f (x)dx pódese aproximar mediante a expresión:
f (x)dx pódese aproximar mediante a expresión:
![]()
![]() .
.