

Informática. Exame de Teoría.
Febreiro, 2006
Nome:
PRIMEIRO PARCIAL:
- (2 PUNTOS) Escribi-las sentencias en Fortran necesarias para chamar a unha función f pasándolle como argumento o nome doutra función g.
- (2 PUNTOS) Escribi-las sentencias en Fortran que permitan: a) abrir un arquivo xa existente (debe producir un erro se o arquivo non existe); b) Ler liñas dende este arquivo, ata atopa-lo final do arquivo. Cada liña debe conter un enteiro de 4 cifras, un real con 3 decimais, un real en forma exponencial con 4 decimais e unha cadea de caracteres.
- (3 PUNTOS) Escribi-lo diagrama de fluxo dun algoritmo que lea por teclado un vector
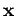 = (x1,..., xn) e calcule o vector transformado
= (x1,..., xn) e calcule o vector transformado
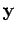 = (y1,..., yn), donde yk (
k = 1,..., n) está dado por:
= (y1,..., yn), donde yk (
k = 1,..., n) está dado por:
yk =
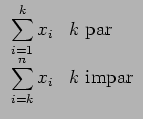
- (1 PUNTO) Escribir unha estrutura de control en Fortran que avalíe o valor dunha variábel enteira e imprima por pantalla grande se o seu valor é meirande ca 100, mediano se está entre 10 e 100, e pequeno se o seu valor é inferior a 10. Non usar sentencias anidadas.
- (2 PUNTOS) Escribir unha subrutina en Fortran que, a partir dunha matriz real cadrada de orde n e dous valores enteiros
1
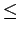 i, j
i, j 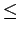 n, proporcione como resultado a suma dos elementos da fila i e da columna j da matriz. Indica-lo tipo dos argumentos da subrutina.
n, proporcione como resultado a suma dos elementos da fila i e da columna j da matriz. Indica-lo tipo dos argumentos da subrutina.
SEGUNDO PARCIAL:
- (2 PUNTOS) Explica qué fan as seguintes sentencias en pseudocódigo. Qué algoritmo implementa este pseudocódigo?
algoritmo xxx
dende i = 1 ata n - 1
aux = x(i)
k = i
dende j = i + 1 ata n
se x(j) < aux
aux = x(j)
k = j
fin_se
fin_dende
x(k) = x(i)
x(i) = aux
fin_dende
fin
- (2 PUNTOS) Escribi-los comandos de Matlab necesarios para representar gráficamente no intervalo
x, y
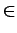 [- 5, 5] a función:
[- 5, 5] a función:
- (1 PUNTO) Dada unha matriz
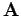 cadrada de orde 5, escribi-los comandos de Matlab que: a) selecciona a submatriz de
cadrada de orde 5, escribi-los comandos de Matlab que: a) selecciona a submatriz de 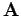 coas filas 2-3 e as columnas 1-3. b) Amplia-la matriz engadíndolle unha fila ao comezo da matriz.
coas filas 2-3 e as columnas 1-3. b) Amplia-la matriz engadíndolle unha fila ao comezo da matriz.
- (2 PUNTO) Escribe unha función en Fortran 90 que reciba como argumentos un punteiro p ao primeiro nodo dunha lista enlazada de enteiros e un enteiro x. A función debe busca-lo enteiro x na lista, e retornar un punteiro ao nodo no que se atopa dito enteiro, ou un punteiro nulo se non o atopa.
- (3 PUNTO) Supoñamos que queremos borra-lo nodo apuntado por q na seguinte lista dobremente enlazada:
Escribi-las sentencias (en pseudocódigo) necesarias para borra-lo nodo e axusta-los punteiros dos elementos da lista para que quede correctamente. NOTA: non temos que busca-lo nodo a borrar: supoñemos que o punteiro q xa apunta ao nodo que queremos borrar.



© 2006, Dr. Manuel Fernández Delgado, Universidade de Santiago de Compostela, Departamento de Electrónica e Computación
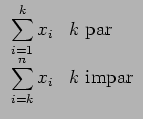
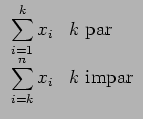
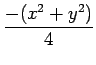
![\includegraphics[width=10cm]{figura.eps}](img11.png)