

Informática. Exame de Prácticas.
Febreiro, 2006
Nome:
Dada unha curva de ecuacións paramétricas
x = x(t), y = y(t) (t é o parámetro), a lonxitude do arco de curva que vai dende o punto
(x(a), y(a)) ao punto
(x(b), y(b)) está dado pola seguinte fórmula:
L = 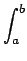 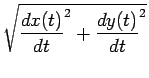 dt dt
|
|
A integral definida dunha función f (x) pódese aproximar como:
Onde n (cun valor elevado) é o número de puntos da partición do intervalo [a, b].
Escribir un programa principal en Fortran que faga o seguinte:
- (6 PUNTOS) Chamar a un subprograma lonxitude_curva(...) (debes decidi-lo tipo de subprograma), que reciba como argumentos o número enteiro n de puntos da partición e os límites a e b do intervalo. O subprograma debe proporcionar como resultado a lonxitude L da curva ``Bruxa de Agnesi'':
| x(t) = 2cotgt |
|
|
(2) |
| y(t) = 1 - cos2t |
|
|
(3) |
para valores de t no intervalo [0,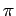 ]. Ademáis, o subprograma debe proporcionar como saída os valores das funcións x(t) e y(t) para valores de
t
]. Ademáis, o subprograma debe proporcionar como saída os valores das funcións x(t) e y(t) para valores de
t 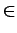 [0,
[0,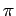 ].
].
- (4 PUNTOS) Chamar a outro subprograma almacena_datos(...) (debes decidi-los seus argumentos e tipo de subprograma), que almacene os valores de t, x(t) e y(t) para
t
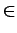 [0,
[0,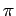 ] (os tres valores na mesma fila), xunto coa lonxitude da curva L, no arquivo datos.dat.
] (os tres valores na mesma fila), xunto coa lonxitude da curva L, no arquivo datos.dat.



© 2006, Dr. Manuel Fernández Delgado, Universidade de Santiago de Compostela, Departamento de Electrónica e Computación
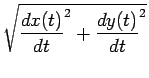 dt
dt
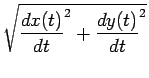 dt
dt
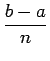
![]() ]. Ademáis, o subprograma debe proporcionar como saída os valores das funcións x(t) e y(t) para valores de
t
]. Ademáis, o subprograma debe proporcionar como saída os valores das funcións x(t) e y(t) para valores de
t ![]() [0,
[0,![]() ].
].