Informática. Exame de Teoría.
Novembro, 2004


Nome:

1. (0.5 PUNTOS) Cáis son as propriedades que debe ter un algoritmo?

   Definido, preciso e finito.

2. (0.5 PUNTOS) Describir brevemente o principio no que se basa o algoritmo de ordeamento por selección.

   Trátase de atopa-lo mínimo dos n elementos a ordear e intercambialo co primeiro elemento (é dicir, situa-lo mínimo na esquerda do vector). Logo, atopa-lo mínimo dos n - 1 elementos restantes, e intercambialo do segundo elemento (é dicir, o elemento mais á esquerda dos n - 1 elementos considerados). Logo, repeti-lo proceso para os n - 1 elementos restantes, e así sucesivamente.

3. (0.75 PUNTOS) Escribir en pseudocódigo e en diagramas de fluxo as estruturas de iteración permitidas en programación estruturada.

   Só as poño en pseudocódigo:

   repetir
     sentencias
   ata que condición
   

   mentres condición
     sentencias
   fin_mentres
   

   dende var = inicial ata final paso n
     sentencias
   fin_dende
   

4. (0.5 PUNTOS) Escribir un segmento de código en Fortran que declare unha matriz de enteiros de orden 3x6 e inicialice os seus elementos de modo que a_ij = ij² - ji², i = 1,..., 3;j = 1,..., 6.

   real, dimension(3, 6) :: m
   
   do i = 1, 2
     do j = 1, 6
       m(i, j) = i*j**j - i*i*j
     end do
   end do
   

5. (0.5 PUNTOS) Ónde se pode usar e para qué serve a sentencia exit?

   Pódese usar nas estruturas do e serve para rompe-la estrutura iterativa.

6. (0.5 PUNTOS) Para qué serve a sentencia parameter?

   Para definir constantes.

7. (0.5 PUNTOS) Cál é a estrutura en Fortran 90 equivalente á seguinte estrutura en pseudocódigo?

   repetir
       sentencias
   ata que condición
   

   Solución:

   do
     sentencias
     if(condición) exit
   end do
   

8. (0.5 PUNTOS) Dado o arrai real, dimension(-4:11) :: x, cántos elementos ten?

   Ten 11 - (- 4) + 1 = 16 elementos.

9. (0.5 PUNTOS) Dada a declaración real, dimension(:), allocatable :: x, qué fai a sentencia allocate(x(n))?

   Reserva memoria dinámicamente para un vector de n elementos reais.

10. (0.75 PUNTOS) Cál é a causa do erro producido polo seguinte segmento de código en Fortran?

    integer, dimension(:), allocatable :: x
    
    do i = 1, 10
      print *, x(i)
    end do
    

    Trátase dun erro de segmentación que se produce na primeira iteración do bucle do, no print, ao tratar de acceder a x(1) sen reservar memoria para o arrai dinámico x.

11. (0.5 PUNTOS) Cómo podemos comprobar se un punteiro apunta a algures?

    Coa función intrínseca associated(p), que volta .true. se o punteiro p apunta a algures, e .false. en caso contrario.

12. (0.75 PUNTOS) Qué imprime por pantalla o seguinte segmento de código?

    integer, dimension(10) :: x
    
    do i = 1, 10
      x(i) = i - 5
    end do
    where(x > 0)
      x = x + 1
    elsewhere
      x = x - 1
    end where
    print *, x
    

    Solución: -5 -4 -3 -2 -1 2 3 4 5 6

13. (0.5 PUNTOS) Escribir un bloque select case que imprima grande se $\sqrt{{x^2 + y^2 + z^2}}$ > a, imprima medio se a > $\sqrt{{x^2 + y^2 + z^2}}$ > b e imprima erro noutro caso ( a, b, x, y, z son variábeis xa declaradas).

    select case (sqrt(x*x + y*y + z*z))
    case (a:)
      print *, "grande"
    case (b:a)
      print *, "medio"
    case default:
      print *, "erro"
    end select
    

    De todos modos, a expresión debería ser enteira, pero non se terá en conta isto na avaliación.

14. (0.5 PUNTOS) Cántas iteracións se executarán no seguinte bucle do?

    do i = 10, -10, -3
      x(i) = i
    end do
    

    Executaranse max[0,(- 10 - 10 - (- 3))/(- 3)] = max(0, 7) = 7

15. (0.5 PUNTOS) Escribir unha función de sentencia que implemente a función: f (x, y, z, t) = exp$\left(\vphantom{ \frac {x^2 + y^2 + z^2} {t^2} }\right.$${\frac{{x^2 + y^2 + z^2}}{{t^2}}}$$\left.\vphantom{ \frac {x^2 + y^2 + z^2} {t^2} }\right)$. Escribir unha sentencia que calcule, usando dita función, exp$\left(\vphantom{ \frac {10^2 + (a + b)^2 + z^2} {5^2} }\right.$${\frac{{10^2 + (a + b)^2 + z^2}}{{5^2}}}$$\left.\vphantom{ \frac {10^2 + (a + b)^2 + z^2} {5^2} }\right)$.

    f(x, y, z, t) = exp((x*x + y*y + z*z)/(t*t))
    f(10, a + b, z, 5)
    

16. (0.5 PUNTOS) Completa os atributos intent dos argumentos no seguinte segmento de código:

    subroutine s(a, b, c, d)
    real, intent(inout) :: a
    real, intent(in) :: b
    real, intent(in) :: c
    real, intent(out) :: d
    print *, a
    a = b + c
    d = a - c
    return
    end subroutine
    

17. (0.5 PUNTOS) Cál será o valor devolto pola seguinte función se x = 1?

    function f(x)
    real, intent(in) :: x
    y = x**3 - 3*x**2 + x - 1
    return
    end function
    

    O valor devolto está indefinido (será lixo) porque nunca se lle da un valor á variábel f, que é a devolta pola función.

18. (0.75 PUNTOS) Escribir una función recursiva en Fortran 90 que implemente a seguinte función:
    f (x) = $$\left\{\vphantom{ \begin{array}{ll} x + f(x - 1) & x > 1 \\ 1 & x = 1 \end{array} }\right.$$$$\begin{array}{ll} x + f(x - 1) & x > 1 \\ 1 & x = 1 \end{array}$$

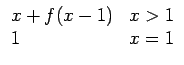
    recursive integer function f(x) result(y)
    integer, intent(in) :: x
    
    if(x > 1) then
      y = x + f(x - 1)
    else
      y = 1
    end if
    return
    end function