Informática. Exame de Prácticas
Febreiro, 2004

NOTA: A nota final é a media dos exames de teoría e prácticas.

1. (4 Puntos) Escribir un programa en Fortran 90 que faga o seguinte:
   • Chamar a un subprograma le_matriz() (cos seus argumentos) que abra un arquivo chamado datos.txt e lea del unha matriz 4x4. Podedes supor que o arquivo datos.txt ten o seguinte contido:

     	9.85 8.23 7.45 1.23
     	2.34 9.01 3.18 0.33
     	3.44 7.81 0.98 7.21
     	1.22 2.31 7.65 4.56
     

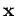
   • Chamar a un subprograma (de qué tipo?) produto_vector_matriz() (tes que decidi-los seus argumentos) que calcule o produto matricial 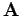$\bf x$$\bf A$, onde 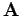$\bf A$ é a matriz lida do arquivo, 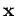$\bf x$ é o vector 1x4 composto pola primeira fila da matriz. Imprimi-lo resultado do produto en pantalla.

   SOLUCIÓN:

     program produto_matriz
   
     real, dimension(4, 4) :: a
     real, dimension(4) :: x, p
     real :: res
   
     call le_matriz(a)
   
     do i = 1, 4
       x(i) = a(1, i)
     end do
   
   * PRODUTO DE x POR a
     do i = 1, 4
       p(i) = 0
         do j = 1, 4
           p(i) = p(i) + x(j)*a(j, i)
         end do
     end do
   
     print *, "O resultado é ", (p(i), i = 1, 4)
     end
   
   
   cccccccccccccccccccccccccccccccccccccccc
     subroutine le_matriz(matriz)
     real, dimension(4, 4), intent(out) :: matriz
   
     open(1, file="datos.txt")
     do i = 1, 4
       read (1, 2) (matriz(i, j), j = 1, 4)
   2 format(4(f4.2, 1x))
     end do
   
     print *, "Matriz lida: "
     do i = 1, 4
       print 2, (matriz(i, j), j = 1, 4)
     end do
   
     close(1)
     return
   1 print *, "Erro en open"
     stop
     end
   

2. (4 Puntos) Escribir un subprograma aproxima_seno() en Fortran 90 que aproxime a función trigonométrica y = f (x) = sen(x) mediante o seu desenrrolo en serie de Taylor:

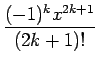
   $$\approx \sum_{{k=0}}^{n} {\frac{{(-1)^k x^{2k+1}}}{{(2k + 1)!}}}$$ (1)

   As entradas do subprograma deben ser o valor de x e a orde n de aproximación. A saída do subprograma debe ser o valor da aproximación no punto x. Necesitarase tamén escribir un subprograma que calcule o factorial dun número enteiro: x! = x(x - 1)(x - 2) ... 1.

   SOLUCIÓN:

     function aproxima_seno(x, n)
     real, intent(in) :: x
     integer, intent(in) :: n
     integer :: k, factorial
   
     aproxima_seno = 0
     do k = 0, n
       aproxima_seno = aproxima_seno + (-1)**k*x**(2*k + 1)/factorial(2*k + 1)
     end do
     return
     end
   
   cccccccccccccccccccccccccccc
     integer function factorial(n)
     integer, intent(in) :: n
   
     factorial = 1
     do i = 2, n
       factorial = factorial*i
     end do
     return
     end
   

3. (2 Puntos) Cuestións de UNIX:
   • Escribir un comando que engada o permiso de escritura sobre tódolos arquivos do directorio actual a tódolos usuarios do mesmo grupo co proprietario.

     SOLUCIÓN: chmod g+w *

   • Escribi-los comandos necesarios para: (1) crear un directorio (2) cambia-lo nome dun arquivo (3) visualizar un arquivo de texto páxina a páxina.

     SOLUCIÓN:

     a) mkdir directorio

     b) mv arquivo_1 arquivo_2

     c) more arquivo