

Informática. Exame de Teoría
Setembro, 2003
- (0.75 PUNTOS) Explica-las diferencias entre un programa compilado e un
interpretado, indicando as vantaxes e inconvintes de cada caso.
- (0.50 PUNTOS) Enumera e explica brevemente os tres tipos de conmutación nunha rede.
- (0.50 PUNTOS) Enumera e describe (1 liña) as etapas do proceso de desenrolo dun
programa.
- (2 PUNTOS) Escribir un programa en seudocódigo que lea por teclado dous números enteiros i e j
entre 1 e 10 (ambos incluidos). Logo, debe calcula-los elementos dunha matriz cadrada de orde
10: os elementos da mesma diagonal co elemento (i, j) deben valer 1, e os restantes deben valer 0.
Por exemplo, se
i = 5, j = 3, a matriz debe ser:
- (0.5 PUNTOS) Converti-lo número 11010101, que se atopa en complemento a dous
(representación de 8 bits), a decimal.
- (0.5 PUNTOS) Realiza-la resta 34 - 15 usando complementos a 1 e representación de 8
bits.
- Escribir-lo(s) comando(s) de Matlab necesarios para:
- (0.75 PUNTOS) Calcula-las seguintes expresións:
- (0.5 PUNTOS) Representar, no intervalo [- 10, 10], a función
f (x) = 1/(1 - x2).
- (0.5 PUNTOS) Ler do arquivo datos.dat unha matriz cadrada 5x5
e calcula-los seus autovalores.
- (0.75 PUNTOS) Obte-los coeficientes do polinomio de orde 5 que mellor
se axusta (minimiza o erro cuadrático medio) a un conxunto de puntos con coordenadas X e Y dadas
polos vectores x e y.
- Cuestións de Fortran:
- (0.50 PUNTOS) Escribir unha función sen argumentos que retorne o número de veces que
foi chamada.
- (0.50 PUNTOS) Indica-la orde na que se executan as seguintes operacións: sqrt(a + b/5*7) -
2/(a + b)**2; x*y**z + abs(x - 5/7 + 2)
- (0.50 PUNTOS) Explicar en qué se diferencian os modos de pasar argumentos a un subprograma en Fortran.
Cál é o modo por defecto?
- (1.25 PUNTOS) Escribir un subprograma que abra un arquivo, xa esistente, con nome igual
ó argumento do subprograma, e lea liñas até a fin do arquivo. Cada liña ten a
seguinte estrutura:
-12.5637*****9823*****Luis Álvarez Yáñez
Cada * é un espacio en branco. Ademais, debe imprimir por pantalla, nese mesmo formato,
os valores lidos. Finalmente, debe pechar o arquivo.



© 2006, Dr. Manuel Fernández Delgado, Universidad de Santiago de Compostela, Departamento de Electrónica e Computación
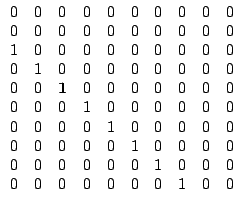
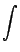 xln(x)dx;
xln(x)dx; 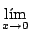
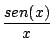 ;
; 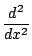
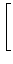 exp
exp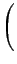 -
- 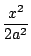
![$\displaystyle \Bigg]$](img12.png)