Informática. Exame de Prácticas
Setembro, 2003

Consideramos un recinto rectangular como o mostrado na figura, modelado como unha matriz cadrada T de orde 10, onde T_ij(t) é a temperatura do elemento ij no instante t. Os elementos situados no rectángulo central atópanse a unha temperatura constante T₁ = 15, e os elementos situados nos bordes da matriz están a T₀ = 0.

Imos simular o comportamento térmico deste rectángulo. En cada instante t, o valor novo T_ij(t + 1) da temperatura no elemento ij calcúlase como o promedio dos valores T_kl(t) asociados ós seus elementos veciños (na figura sinalados cun rombo discontinuo) e a el mesmo. Ten en conta que os elementos situados no borde da matriz e no rectángulo interior (zonas sombreadas) teñen unha temperatura constante (T₀ ou T₁) durante todo o proceso. É dicir:

T_ij(t) = $$\left\{\vphantom{ \begin{array}{cc} T_0 & \textrm{elemento $ij$\ ... ...ral} \\ T_1 & \textrm{elemento $ij$\ no borde da matriz} \end{array} }\right.$$$$\begin{array}{cc} T_0 & \textrm{elemento $ij$\ no rect\'{a}ngulo central} \\ T_1 & \textrm{elemento $ij$\ no borde da matriz} \end{array}$$

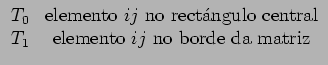
O programa debe chamar a un subprograma que dea valores iniciais (t = 0) á matriz T, indicados pola ecuación anterior, sendo T_ij(t = 0) = 0 para os elementos fora das zonas sombreadas. Logo, debe chamar a un subprograma que actualice a matriz T seguindo a regra descrita no párrafo anterior para calcular T_ij(t + 1) a partir de T_ij(t) e dos T_kl(t) dos seus veciños. Ademais, debe haber outro subprograma que imprima (liña a liña) a matriz T en cada instante t. Entón, o programa debe preguntar ó usuario se quere continuar ou desexa rematar e, no primeiro caso, repetir o cálculo e impresión de T.