f (x) = 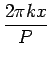 |
(1) |
A Serie de Fourier dunha función periódica f (x) par (isto é, f (- x) = f (x)) de período P está determinada pola seguinte expresión:
f (x) = 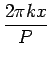 |
(1) |
Onde:
|
a0 = |
(2) |
As integrais pódense aproximar empregando a Regra de Simpson:
ti = a + 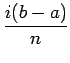 , i = 1, 2,..., n - 1, n , i = 1, 2,..., n - 1, n
|
(4) |
Onde os ti son os n puntos na partición do intervalo [a, b] e
![]() designa á suma dende i = 2 ata n con incrementos de 2:
designa á suma dende i = 2 ata n con incrementos de 2:
|
|
(5) |
Escribir un programa en Fortran que calcule os valores
ak, k = 0,..., K para
f (t) = cos(t), P = 2![]() . Para esto:
. Para esto:
![[*]](crossref.png) . Os argumentos do subprograma deben ser os límites de integración a, b e o número n de puntos no intervalo [a, b] (empregar n = 100).
. Os argumentos do subprograma deben ser os límites de integración a, b e o número n de puntos no intervalo [a, b] (empregar n = 100).
![[*]](crossref.png) . Os argumentos deberán ser os mesmos que no apartado anterior, ademais do índice k.
. Os argumentos deberán ser os mesmos que no apartado anterior, ademais do índice k.
Para
f (t) = cos(t) e P = 2![]() , o resultado debe ser a1 = 1 e
ak = 0, k
, o resultado debe ser a1 = 1 e
ak = 0, k![]() 1.
1.
SOLUCIÓN:
program serie_fourier
parameter (PI = 3.141592)
real integral1, integral2
p = 2*PI; n = 100
a = 2*integral1(0., p, n)/p
print 3, "a0 = ", a
3 format(a5, f8.5)
do 1 k = 1, 10
a = 2*integral2(0., p, k, n)/p
1 print 2, "a", k, " = ", a
2 format(a1, i2, a3, f8.5)
stop
end
cccccccccccccccccccccccccccc
real function integral1(a, b, n)
f(t) = cos(t)
h = (b - a)/n
integral1 = f(a) + f(b)
do 1 i = 2, n, 2
1 integral1 = integral1 + 4*f(a + (i - 1)*h)
do 2 i = 2, n - 2, 2
2 integral1 = integral1 + 2*f(a + i*h)
integral1 = h*integral1/3
return
end
cccccccccccccccccccccccccccc
real function integral2(a, b, k, n)
f(t) = cos(t)*cos(k*t)
h = (b - a)/n
integral2 = f(a) + f(b)
do 1 i = 2, n, 2
1 integral2 = integral2 + 4*f(a + (i - 1)*h)
do 2 i = 2, n - 2, 2
2 integral2 = integral2 + 2*f(a + i*h)
integral2 = h*integral2/3
return
end